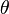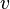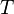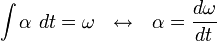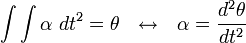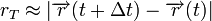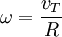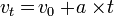Rumus- rumus Fisika

Kamis, 29 November 2012

Dinamika Partikel

Dinamika partikel

Hukum 1 Newton:

Hukum I newton disebut juga hukum kelembaman (inersia).sifat kelembaman benda adalah sifat mempertahankan keadaanya, yaitu keadaaan tetap diam ataukeadaan tetap bergerak beraturan.

∑F= 0
http://www.scribd.com/doc/7976284/Dinamika-partikel

Hukum 2 Newton:

Rumus:

http://modulfisika.blogspot.com/2010/05/kelas-viii-hukum-ii-newton.html

Hukum 3 Newton:

Rumus:

http://modulfisika.blogspot.com/2010/05/kelas-viii-hukum-iii-newton.html

Gerak Melingkar

Gerak Melingkar Beraturan

Gerak suatu benda yang membentuk lintasan dan lintasan tersebut berbentuk l;ingkaran (melingkar) mengelilingi suatu titik tetap.

melingkar membutuhkan gaya, gaya tersebut dinamakan: Gaya sentripetal.
gerakan ini mempunyai kecepatan yang dipercepat beraturan.

Besaran gerak melingkar:

**Besaran gerak lurus dan melingkar**
Gerak lurus		Gerak melingkar
Besaran	Satuan (SI)	Besaran	Satuan (SI)
poisisi $r\!$	m	sudut $\theta\!$	rad
kecepatan $v\!$	m/s	kecepatan sudut $\omega\!$	rad/s
percepatan $a\!$	m/s²	percepatan sudut $\alpha\!$	rad/s²
-	-	perioda $T\!$	s
-	-	radius $R\!$	m

$\int \omega\ dt = \theta \ \ \leftrightarrow\ \ \omega = \frac{d\theta}{dt}$

$\int \alpha\ dt = \omega \ \ \leftrightarrow\ \ \alpha = \frac{d\omega}{dt}$

$\int \int \alpha\ dt^2 = \theta \ \ \leftrightarrow\ \ \alpha = \frac{d^2\theta}{dt^2}$

$\theta = \frac{r_T}{R}\ \ , \ \ \omega = \frac{v_T}{R}\ \ , \ \ \alpha = \frac{a_T}{R}$
$r_T \approx |\overrightarrow{r}(t+\Delta t)-\overrightarrow{r}(t)|\!$

Jenis gerak melingkar
yaitu melingkar beraturan

Rumus:

$\omega = \frac {v_T} R$

http://id.wikipedia.org/wiki/Gerak_melingkar

Besaran Vektor

Besaran Vektor

Besaran vektor: besaran yang memiliki besar dan arah.
vektor: suatu besaran yang memilikki magnitudo dan arah sekaligus

Rumus:

http://idayudi.wordpress.com/fisika-x/vektor/

http://kampoengti.blogspot.com/2010/01/besaran-vektor-dan-skalar.html

Gerak Lurus

Gerak Lurus

http://r4dh1.wordpress.com/2010/05/13/kinematika-gerak-lurus/

GLB (Gerak lurus beraturan)
gerak ini mempunyai kecepatan konstan, maka nilai percepatan a=0.

Rumus: $\!v=\frac{s}{t}$

- v: kecepatan
- s: jarak yang ditempuh
- t: waktu tempuh

Kecepatan rata- rata:
Rumus: $\!v=\frac{s_{total}}{t_{total}} = \frac {V_{1} \times t_{1} + V_{2} \times t_{2} + ... + V_{n} \times t_{n}} {t_{1} + t_{2} + ... + t_{n}}$

GLBB (Gerak lurus berubah beraturan)
gerak berupa garis lurus yang kecepatannya berubah tetapi beraturan

Rumus:
- $\!v_{t}=\!v_{0}+\!a\times\!t$
- $\!s=\!v_{0}\times\!t+\frac{1}{2}\times\!a\times\!t^2$
- $\!v_{t}^2=\!v_{0}^2+\!2\times\!a\times\!s$

v0: kecepatan awal
vt: kecepatan akhir
a: percepatan
s: jarak yang ditempuh

http://id.wikibooks.org/wiki/Rumus-Rumus_Fisika_Lengkap/Gerak

Besaran & Satuan

Besaran: segala sesuatu yang dapat diukur, dihitung yang berbentuk angka dan punya satuan.
Syarat- syarat besaran:
1. dapat diukur dan dihitung
2. dapat dinyatakan dengan angka / punya nilai
3.mempunyai satuan

besaran ini dibedakan menjadi 2 yaitu
a) besaran fisika: diperoleh dari pengukuran
b) besaran non-fisika: diperoleh dari perhitungan

besaran fisika sendiri dibagi menjadi 2 yaitu:
a) besaran pokok: besaran yang ditentukan lebih dulu berdasarkan kesepatan para ahli fisika
b) besaran turunan: besaran yang diturunkan oleh besaran pokok

http://physics-sogzzz.blogspot.com/2010/12/besaran-dan-satuan.html

Pages